|
MetricKnn
Fast Similarity Search using the Metric Space Approach
|
|
MetricKnn
Fast Similarity Search using the Metric Space Approach
|
MetricKnn is an open source library to address the problem of similarity search, i.e., to efficiently locate objects that are close to each other according to some distance function. MetricKnn is comprised of:
The intended users are software developers, academics, students and data scientist who need to efficiently compare objects according to some criteria.
In the following sections you can read More Information about Metric Spaces and MetricKnn library.
The lastest version can be downloaded from SourceForge website:
The source code is available in GitHub. Click here to browse the repository.
MetricKnn is an open source project released under the BSD 2-Clause License.
You can send any question, problem, bug report or comment by creating a new issue in project's page or by email to my address.
MetricKnn is an effort for developing an efficient and ready-to-use tool to resolve similarity searches using the metric space approach. The intended users are researchers and software developers who needs to resolve similarity searches but are not necessarily involved in the indexing research field.
The development of MetricKnn is currently supported by the chilean private research center ORAND S.A. Chile and is partially funded by project Conicyt PAI-781204026..
Currently, we are working on producing a stable version of the library, thereafter more features and algorithms will be released. In future releases, we plan to include:
MetricKnn follows the Metric Space approach, therefore potentially it can resolve searches for any kind of object (either vectors, strings, matrices, bit sequences, graphs, etc.), as long as the distance function returns a distance value for any pair of objects (i.e., a positive floating point number). In order to efficiently resolve exact searches, the distance must be a metric, i.e., it must satisfy the metric properties.
MetricKnn includes an implementation for two Metric Access Methods: LAESA and SnakeTable. It contains also an interface for using FLANN library, which provides the implementation for some multidimensional indexes (kd-tree, k-means tree, LSH).
The similarity search relates to the algorithms to efficiently locate and retrieve similar objects, i.e. objects at a small distance from each other.
For example, if you have the spatial location of all the supermarkets (x-y coordinates), how can you locate the nearest supermarket to your current location? The first approach is to compute the distance from your current location to each supermarket, and then select the one with the lowest distance to you. However, you can achieve a much better performance if the supermarkets are grouped by by spatial location, then during the search you'll have to compute less distances to locate the nearest one. The idea is that if you are far from supermarket C, then you are also far from all the supermarkets that are close to C. The similarity search focuses on those techniques for efficient ordering of objects and fast search algorithms.
Another example from the multimedia field, you have received a picture from a friend and you remember that you already have an almost identical image, but your photo collection is very-large and unsorted. How can you locate the picture that is very similar to the one you have? The common techniques compute some visual feature from all the images (e.g. a color histogram) and build an index of visual features. The search algorithm locates the image whose visual feature is the closest to your picture (according to some distance function). The similarity search focuses on those algorithms for building the index and resolving the search.
A common approach to resolve similarity searches is to model data as multidimensional vectors. In this case the search consists in locating close vectors according to the euclidean distance or some other Minkowski distance. The multidimensional indexes are based on comparing coordinate values and grouping vectors, e.g. the R-tree and k-d tree.
The metric space is a generalization of vector space where there is no coordinates but only a distance function to compare objects. In this approach, the index structures are based on selecting objects (known as pivots) which are compared to the rest of the objects to create groups.
The Metric Access Methods (MAMs) are index structures designed to efficiently perform similarity searches. MAMs avoid a linear scan over the whole database by using the metric properties to save distance computations at the cost of storing some previously computed distances. MAMs differ in their methods for grouping objects and for selecting pivots.
Given the domain \( \cal D \) and the metric distance \( d: { \cal D } \times { \cal D } \rightarrow {\mathbb{R}} \) the object-pivot distance constraint guarantees that:
\[ \forall a,b,p \in { \cal D } \;,\;\; |d(a,p)-d(b,p)| \leq d(a,b) \leq d(a,p)+d(b,p) \]
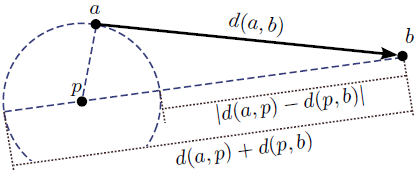
This constraint implies that for any two objects \( a \) and \( b \), a lower bound and an upper bound for \( d(a,b) \) can be calculated using a third object \( p \), which is called a pivot. If \( d(a,p) \) and \( d(b,p) \) are precalculated, then these bounds can be efficiently computed.
Given a collection of objects \( \cal R \) and a set of pivot objects \( \cal P \) (which may or may not be a subset of \( \cal R \)), a pivot table is a \( | {\cal R} | \times | {\cal P} | \) matrix that stores the distance from each pivot to every object in the collection. The similarity search for a query object \( a \) evaluates the distance \( d(a,p) \) for each pivot \( p \in {\cal P} \), and then sequentially scans each object \( b \in {\cal R} \), calculating the lower bound:
\[ d'(a,b) = \max_{p \in \cal P} \left\{ |d(a,p)-d(b,p)| \right\} \leq d(a,b) \]
The value \( d'(a,b) \) can be evaluated efficiently because \( d(a,p) \) is already calculated and \( d(b,p) \) is stored in the pivot table. In the case of range searches, if the lower bound is greater than search range then \( b \) can be safely discarded. In the case of \( k \)-NN searches, if the lower bound is greater than the current \( k \)-th nearest neighbor candidate then \( b \) can be safely discarded. If \( b \) could not be discarded, the actual distance \( d(a,b) \) must be evaluated to decide whether or not \( b \) is part of the search result.
The most evident benefit of using the metric space approach is that it is possible to directly index other objects apart from vectors (like strings, graphs, etc.). The distance function can directly compare objects instead of first computing vectors to describe them (in fact, that process may turn out to be very difficult for some domains).
Additionally, if we intend to work exclusively with vectors (which is a common case for multimedia objects), the comparison of the two approaches should consider two aspects:
There are some libraries for addressing similarity searches:
MetricKnn was created from the search algorithms in P-VCD, which in turn is the result of the PhD thesis work Content-Based Video Copy Detection.
MetricKnn has been developed (and re-used) during different participations at TRECVID workshop since year 2010. The papers and slides describing our participations at TRECVID can be downloaded from its website, teams ORAND and PRISMA-University of Chile.
Some resources to deepen into the similarity search problem:
 1.8.9.1
1.8.9.1